Trazado de Líneas Equipotenciales

Nota: Traer una hoja de papel vegetal o similar de 50 x 35 cm (uno por comisión)

El objeto del trabajo es estudiar cualitativamente el campo electrostático en dos dimensiones con condiciones de borde determinadas y obtener un mapa de líneas de igual potencial.

En el vacío y sin presencia de cargas libres, el potencial electrostático V verifica la ecuación de Laplace:

[1]

y el potencial V esta relacionado con el campo electrostático por:

[2]

Para conocer el potencial V=V(x, y, z) en una región determinada del espacio se debe resolver la ecuación [1]:

[3]

teniendo en cuenta las condiciones de borde del problema. Estas condiciones pueden hacer sumamente dificultosa, o imposible, la resolución analítica del problema, por lo que se deben usar métodos analógicos o numéricos.

Resolver un problema por un método analógico significa trasladarlo a otro sistema que responda formalmente a las mismas ecuaciones, pero cuya resolución practica sea sencilla. En nuestro caso consideraremos la distribución del potencial eléctrico en un medio conductor con una distribución de corrientes estacionaria. La ecuación de continuidad es:

[4]

usando la ley de Ohm:

[5]

la ecuación [4] se escribe:

[6]

como

[7]

o [8]

Así resulta que la ecuación [8] es idéntica a la [1].

Podemos establecer, entonces, una analogía entre las líneas de campo electrostático y las líneas de corriente eléctrica; la diferencia de potencial electrostático y la caída de potencial en el material conductor.

De acuerdo a la analogía establecida, trabajaremos sobre papel conductor de alta resistividad (papel con una película de grafito), sobre el que dibujamos, con pintura metálica, la configuración que deseamos analizar (superficies equipotenciales que constituyen las condiciones de borde del problema): placas, esferas, etc..

Con una batería se imponen los potenciales deseados a la configuración (a escala con el problema real) y por el papel conductor se completará el circuito, estableciéndose líneas de corriente y produciéndose caídas de potencial de manera que se cumple la ecuación de Laplace.

Los puntos de igual potencial se buscan con una punta de prueba y un voltímetro digital, según indica la figura.

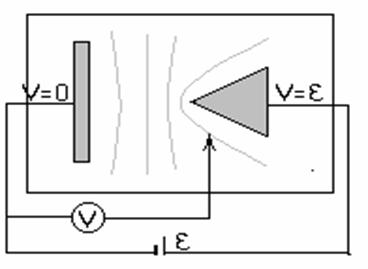Figura 1

Para resolver en forma numérica, consideraremos al plano (continuo) como un conjunto discreto de puntos separados una distancia Dx = Dy = d uno de otro, de manera de trabajar con incrementos finitos en lugar de diferenciales.

[9]

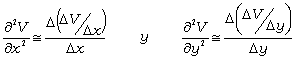[10]

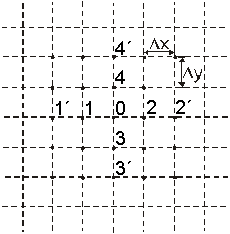Figura 2

La ecuación [3] en un punto cualquiera que llamaremos 0 es:

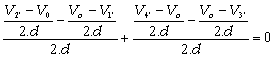[11]

o sea:

[12]

Lo que nos dice que el potencial en cualquier punto debe ser igual al promedio de los potenciales de los cuatro puntos próximos separados a distancias 2d. Como la elección de d es arbitraria (lo suficientemente pequeña para que la aproximación por incrementos finitos sea válida), entonces:

[13]

Siguiendo un método iterativo con un programa que trabaja con una matriz de puntos (en nuestro caso 101 x 161), hallamos los potenciales de los mismos. Los datos a ingresar son los de la configuración, admitiendo el programa placas y círculos con potencial impuesto (dado) o cuyo valor quede determinado por la solución del problema (es decir elementos que deformen el campo originado por aquellos que tienen potencial fijo).