Deducción de la
fórmula de la
Aceleración Normal
Galileo y Descartes ya reconocieron que una partícula
que describe un movimiento circular
uniforme tiene aceleración. Huygens fue el primero que
resolvió este problema. Sin embargo, el procedimiento empleado por Newton para
deducir la fórmula de la aceleración normal tiene la ventaja de ser mucho más
fácil de entender.
La deducción de la fórmula de la aceleración normal se
basa en el análisis de la trayectoria poligonal que sigue una partícula que
choca contra una superficie cilíndrica. Esta deducción no debe tomarse de forma
rigurosa sino como un ejercicio de importancia histórica.
Deducción de la fórmula de la aceleración normal por
Newton
Como veremos en esta deducción, lo importante es el
cambio en la dirección de la velocidad, no la causa que produce este cambio, ya
sea el choque con la superficie rígida, la acción de la gravedad, etc.
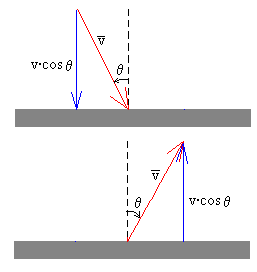
Consideremos una partícula que se mueve en línea recta con velocidad constante v y que choca contra una superficie rígida. Como vemos en la figura la componente de la velocidad v que es perpendicular a la superficie v·cosq cambia de sentido en el momento del impacto. Sin embargo, la componente que es paralela a la superficie v·senq no cambia durante el impacto.
El cambio de velocidad que experimenta la partícula en
el choque contra la superficie rígida es
Dv=2vcosq
Supongamos ahora que la superficie rígida tiene adopta
la forma cilíndrica de radio r.
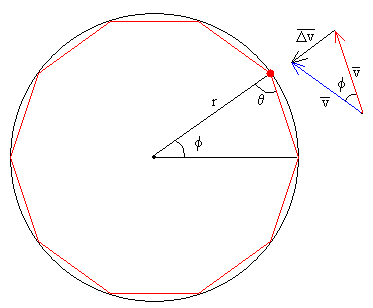
El cambio de velocidad en cada impacto Dv, es la diferencia entre la velocidad final v’
(en color azul) y la velocidad inicial v (en color rojo). La dirección
de dicho cambio de velocidad Dv es radial y apunta
hacia el centro de la trayectoria que describe la partícula. Su módulo vale
![]()
Esta misma expresión se puede deducir en el diagrama
de velocidades, calculando el lado Dv del triángulo isósceles de vértice f que forman los vectores velocidad antes y después del impacto.
La aceleración media para n impactos
La velocidad de la partícula es constante en los
tramos rectos y por tanto, la aceleración es nula. Cuando choca con la
superficie rígida la partícula cambia bruscamente la dirección de su velocidad aunque
no su módulo y la aceleración en el instante del impacto es infinita. La
aceleración media como veremos nos conduce a la fórmula de la aceleración
normal.
Después de n impactos contra la superficie
rígida, la partícula describe una trayectoria que es un polígono regular de n
lados. Teniendo en cuenta que el ángulo f =2p/n. El cambio total
de velocidad que experimenta la partícula tras n impactos es
![]()
Calculamos ahora el tiempo que tarda la partícula en
describir la trayectoria, un polígono regular de n lados.
En el triángulo isósceles formado por un lado y dos
radios, calculamos el valor del lado, conociendo el ángulo f del vértice. La longitud del perímetro del polígono regular es
![]()
La partícula en cada impacto cambia la dirección de su
velocidad pero no cambia su módulo. Por tanto, el tiempo que invierte en
recorrer la trayectoria poligonal es P=l/v
El valor medio del módulo de la aceleración es
![]()
La aceleración media para infinitos impactos
El cambio total de velocidad que experimenta la
partícula tras n impactos es
![]()
Cuando n es muy grande (tiende a infinito) el
ángulo es muy pequeño y podemos
sustituir el seno por el ángulo. De modo que, el cambio total de velocidad que
experimenta la partícula es
![]()
Cuando n es muy grande (tiende a infinito) el
perímetro del polígono regular (trayectoria) que describe la partícula se
aproxima a una circunferencia de radio r.
Como el módulo de la velocidad de la partícula v
no cambia en los impactos con la pared rígida, el tiempo P que tarda en
describir la circunferencia es
![]()
El módulo de la aceleración media es
![]()
Dada la simetría de la trayectoria circular, la
aceleración media es la aceleración de la partícula en cada instante
![]()