Deducción alternativa
de las fórmulas de la aceleración tangencial y normal
Es interesante explorar
otras deducciones alternativas de las fórmula de la
aceleración normal. En este caso se presenta una deducción que tiene la ventaja
de que se puede extender a movimientos circulares no uniformes. Estas
deducciones se pueden comparar con las realizadas en las páginas tituladas
"Relación entre las magnitudes
angulares y lineales" y Deducción de la fórmula de la
aceleración normal siguiendo el procedimiento
de Newton.
Movimiento circular uniforme
Consideremos que una partícula
describe un movimiento circular de radio r con velocidad constante v.
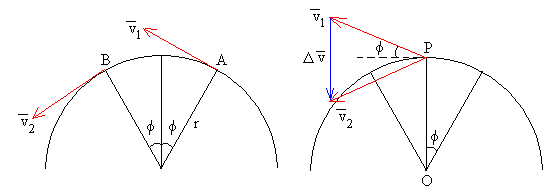
La partícula se encuentra en
la posición A en el instante t-t/2, y su velocidad (tangente a la trayectoria) es v1. La partícula se encuentra en la posición
simétrica B en el instante t+t/2 y su velocidad es v2.
Coloquemos los dos vectores
velocidad v1 y v2 que tienen la misma
longitud v con vértice en el punto P y calculamos las componentes radial
o normal y tangencial del vector diferencia v=v2-v1.
- Componente normal
(v)n=v2·sen -v1·sen(- )=2v·sen
- Componente tangencial
(v)t=v2·cos -v1·cos(- )=0
Por tanto el vector v es paralelo a la dirección radial PO, y
está dirigido hacia el centro O.
Como la partícula recorre el
arco AB de ángulo 2 con
velocidad v constante.
![]()
El valor medio de la
componente normal de la aceleración es por tanto,
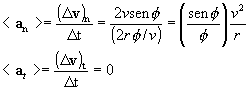
La componente normal de la
aceleración instantánea es el límite de la aceleración media cuando el
intervalo de tiempo t 0, o bien cuando 0. En este límite, sen / 1 y por tanto, la componente normal de la
aceleración en el instante t o en el punto P es
![]()
Naturalmente, la componente
tangencial de la aceleración es cero en dicho instante, at=0.
Movimiento circular no
uniforme
Supongamos que la partícula
pasa por el punto A en el instante t-t1 y
lleva una velocidad v1 (tangente a la trayectoria), y pasa
por el punto simétrico B en el instante t-t2 llevando una velocidad v2.
Como el movimiento no es uniforme los módulos de las velocidades serán
diferentes.
Calculamos las componentes
radial o normal y tangencial del vector diferencia v=v2-v1.
- Componente normal
(v)n=v2·sen -v1·sen(- )=2(v2+v1)·sen
- Componente tangencial
(v)t=v2·cos -v1·cos(- )= (v2-v1) cos
Al no ser los vectores
velocidad de igual módulo, el vector diferencia v y por tanto la aceleración no tienen en
general, dirección radial.
La partícula recorre el arco
AB de ángulo 2 empleando un tiempo t=t1+ t2. La velocidad media <v> de la
partícula en este intervalo de tiempo es
![]()
La componente normal y
tangencial de la aceleración serán por tanto,
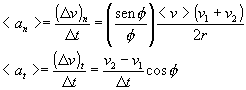
En el límite cuando el
intervalo de tiempo t 0, o bien cuando 0, se cumple que, sen / 1, cos 1. La velocidad media <v> v es la velocidad en
el instante t cuando el móvil pasa por P, y también la velocidad
promedio (v1+v2)/2 v.
De este modo obtenemos la
misma fórmula de la componente normal de la aceleración que en el apartado
anterior.
En cuanto a la componente
tangencial, el numerador es un cambio infinitesimal en el módulo de la
velocidad dv y el denominador es el tiempo dt que tarda la
partícula en efectuar dicho cambio.
Las componentes de la
aceleración serán, por tanto,
![]()
Deducción alternativa de las
fórmulas de la aceleración tangencial y normal
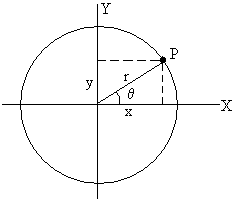
En la figura la partícula se encuentra en el instante t en el punto P, formando un ángulo con el eje X.
El vector posición r
de la partícula es
r=xi+yj=r·cos
i+r·sen j
El vector velocidad v se
obtiene derivando el vector posición respecto del tiempo
![]()
El vector aceleración se
obtiene derivando el vector velocidad
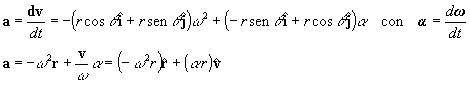
El vector aceleración tiene
dos componentes, que podemos expresar en virtud de las relaciones entre magnitudes
angulares y lineales de dos formas.
La componente radial está
dirigida hacia le centro de la circunferencia
an=2r=v2/r,
La componente tangencial
tiene la dirección de la velocidad, tangente a la trayectoria
at=
r=dv/dt.
Referencias
Leff
H. Acceleration for circular motion. Am. J. Phys. 70 (5) May
2002.