El rozamiento por deslizamiento

El rozamiento entre dos superficies en contacto ha sido aprovechado por nuestros antepasados más remotos para hacer fuego frotando maderas. En nuestra época, el rozamiento tiene una gran importancia económica, se estima que si se le prestase mayor atención se podría ahorrar muchísima energía y recursos económicos.

Históricamente, el estudio del rozamiento comienza con Leonardo da Vinci que dedujo las leyes que gobiernan el movimiento de un bloque rectangular que desliza sobre una superficie plana. Sin embargo, este estudio pasó desapercibido.

En el siglo XVII Guillaume Amontons, físico francés, redescubrió las leyes del rozamiento estudiando el deslizamiento seco de dos superficies planas. Las conclusiones de Amontons son esencialmente las que estudiamos en los libros de Física General:

• La fuerza de rozamiento se opone al movimiento de un bloque que desliza sobre un plano.
• La fuerza de rozamiento es proporcional a la fuerza normal que ejerce el plano sobre el bloque.
• La fuerza de rozamiento no depende del área aparente de contacto.

El científico francés Coulomb añadió una propiedad más

• Una vez empezado el movimiento, la fuerza de rozamiento es independiente de la velocidad.

Explicación del origen del rozamiento por contacto

La mayoría de las superficies, aún las que se consideran pulidas son extremadamente rugosas a escala microscópica. Los picos de las dos superficies que se ponen en contacto determinan el área real de contacto que es una pequeña proporción del área aparente de contacto (el área de la base del bloque). El área real de contacto aumenta cuando aumenta la presión (la fuerza normal) ya que los picos se deforman.

Los metales tienden a soldarse en frío, debido a las fuerzas de atracción que ligan a las moléculas de una superficie con las moléculas de la otra. Estas soldaduras tienen que romperse para que el deslizamiento se presente. Además, existe siempre la incrustación de los picos con los valles. Este es el origen del rozamiento estático.

Cuando el bloque desliza sobre el plano, las soldaduras en frío se rompen y se rehacen constantemente. Pero la cantidad de soldaduras que haya en cualquier momento se reduce por debajo del valor estático, de modo que el coeficiente de rozamiento dinámico es menor que el coeficiente de rozamiento estático.

Finalmente, la presencia de aceite o de grasa en las superficies en contacto evita las soldaduras al revestirlas de un material inerte.

La explicación de que la fuerza de rozamiento es independiente del área de la superficie aparente de contacto es la siguiente:

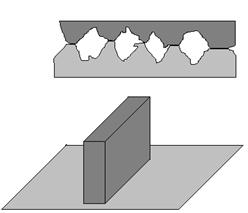
En la figura, la superficie más pequeña de un bloque está situada sobre un plano. En el dibujo situado arriba, vemos un esquema de lo que se vería al microscopio: grandes deformaciones de los picos de las dos superficies que están en contacto. Por cada unidad de superficie del bloque, el área de contacto real es relativamente grande (aunque esta es una pequeña fracción de la superficie aparente de contacto, es decir, el área de la base del bloque).

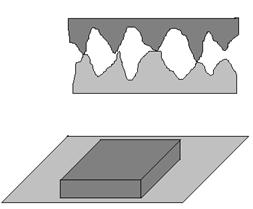
En la figura, la superficie más grande del bloque está situada sobre el plano. El dibujo muestra ahora que las deformaciones de los picos en contacto son ahora más pequeñas por que la presión es más pequeña. Por tanto, un área relativamente más pequeña está en contacto real por unidad de superficie del bloque. Como el área aparente en contacto del bloque es mayor, se deduce que el área real total de contacto es esencialmente la misma en ambos casos.

Ahora bien, las investigaciones actuales que estudian el rozamiento a escala atómica demuestran que la explicación dada anteriormente es muy general y que la naturaleza de la fuerza de rozamiento es muy compleja.

La fuerza normal

La fuerza normal, reacción del plano o fuerza que ejerce el plano sobre el bloque depende del peso del bloque, la inclinación del plano y de otras fuerzas que se ejerzan sobre el bloque.

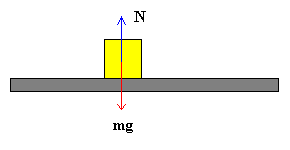
Supongamos que un bloque de masa m está en reposo sobre una superficie horizontal, las únicas fuerzas que actúan sobre él son el peso mg y la fuerza y la fuerza normal N. De las condiciones de equilibrio se obtiene que la fuerza normal N es igual al peso mg

N=mg

Si ahora, el plano está inclinado un ángulo q , el bloque está en equilibrio en sentido perpendicular al plano inclinado por lo que la fuerza normal N es igual a la componente del peso perpendicular al plano, N=mg·cosq

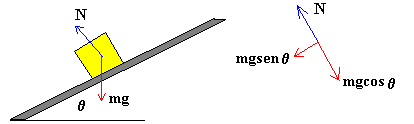
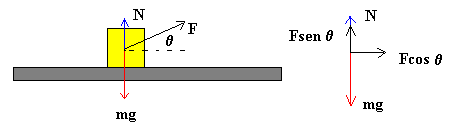
Consideremos de nuevo el bloque sobre la superficie horizontal. Si además atamos una cuerda al bloque que forme un ángulo q con la horizontal, la fuerza normal deja de ser igual al peso. La condición de equilibrio en la dirección perpendicular al plano establece N+ F·senq =mg

Fuerza de rozamiento dinámico

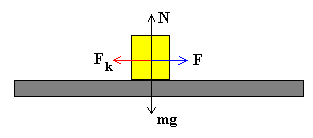
En la figura, se muestra un bloque arrastrado por una fuerza F horizontal. Sobre el bloque actúan el peso mg, la fuerza normal N que es igual al peso, y la fuerza de rozamiento F_k entre el bloque y el plano sobre el cual desliza. Si el bloque desliza con velocidad constante la fuerza aplicada F será igual a la fuerza de rozamiento F_k.

Podemos investigar la dependencia de F_k con la fuerza normal N. Veremos que si duplicamos la masa m del bloque que desliza colocando encima de éste otro igual, la fuerza normal N se duplica, la fuerza F con la que tiramos del bloque se duplica y por tanto, F_k se duplica.

La fuerza de rozamiento dinámico F_k es proporcional a la fuerza normal N.

F_k=m_k N

La constante de proporcionalidad m_k es un número sin dimensiones que se denomina coeficiente de rozamiento dinámico.

El valor de m_k es casi independiente del valor de la velocidad para velocidades relativas pequeñas entre las superficies, y decrece lentamente cuando el valor de la velocidad aumenta.

Fuerza de rozamiento estático

También existe una fuerza de rozamiento entre dos objetos que no están en movimiento relativo.

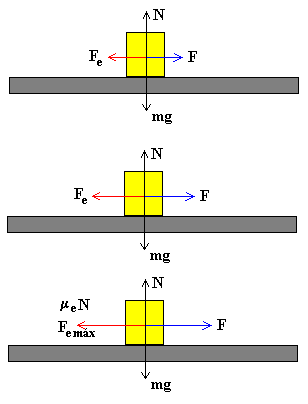
Como vemos en la figura la fuerza F aplicada sobre el bloque aumenta gradualmente, pero el bloque permanece en reposo. Como la aceleración es cero la fuerza aplicada es igual y opuesta a la fuerza de rozamiento estático F_e.

F=F_e

La máxima fuerza de rozamiento corresponde al instante en el que el bloque está a punto de deslizar.

F_{e máx=}m_eN

La constante de proporcionalidad m_e se denomina coeficiente de rozamiento estático.

Los coeficientes de rozamiento estático y dinámico dependen de las condiciones de preparación y de la naturaleza de las dos superficies y son casi independientes del área de la superficie de contacto.

Comportamiento de un cuerpo que descansa sobre un plano horizontal

Dibujemos una gráfica en la que en el eje horizontal representamos la fuerza F aplicada sobre el bloque y en el eje vertical la fuerza de rozamiento.

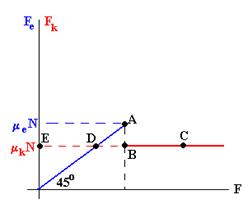
1. Desde el origen hasta el punto A la fuerza F aplicada sobre el bloque no es suficientemente grande como para moverlo. Estamos en una situación de equilibrio estático

F= F_e<m_eN

En el punto A, la fuerza de rozamiento F_e alcanza su máximo valor m_eN

F= F_{e máx=}m_eN

2. Si la fuerza F aplicada se incrementa un poquito más, el bloque comienza a moverse. La fuerza de rozamiento disminuye rápidamente a un valor menor e igual a la fuerza de rozamiento dinámico, F_k=m_k N

Si la fuerza F no cambia, punto B, y permanece igual a F_{e máx} el bloque comienza moviéndose con una aceleración

a=(F-F_k)/m

Si incrementamos la fuerza F, punto C, la fuerza neta sobre el bloque F-F_k se incrementa y también se incrementa la aceleración.

En el punto D, la fuerza F aplicada es igual a F_k por lo que la fuerza neta sobre el bloque será cero. El bloque se mueve con velocidad constante.

En el punto E, se anula la fuerza aplicada F, la fuerza que actúa sobre el bloque es - F_k, la aceleración es negativa y la velocidad decrece hasta que el bloque se para.

Tablas de valores de los coeficientes

• Coeficientes de rozamiento dinámico para diferentes materiales

Superficies en contacto	Coeficiente dinámico mk
Acero sobre acero	0.18
Acero sobre hielo (patines)	0.02-0.03
Acero sobre hierro	0.19
Hielo sobre hielo	0.028
Patines de madera sobre hielo y nieve	0.035
Goma (neumático) sobre terreno firme	0.4-0.6
Correa de cuero (seca) sobre metal	0.56
Bronce sobre bronce	0.2
Bronce sobre acero	0.18
Roble sobre roble en la dirección de la fibra	0.48

Fuente: Koshkin, Shirkévich. Manual de Física Elemental. Editorial Mir 1975.

• Coeficientes de rozamiento estático y dinámico

Superficies en contacto	Coeficiente estático me	Coeficiente dinámico mk
Cobre sobre acero	0.53	0.36
Acero sobre acero	0.74	0.57
Aluminio sobre acero	0.61	0.47
Caucho sobre concreto	1.0	0.8
Madera sobre madera	0.25-0.5	0.2
Madera encerada sobre nieve húmeda	0.14	0.1
Teflón sobre teflón	0.04	0.04
Articulaciones sinoviales en humanos	0.01	0.003

Fuente: Serway. Física. Editorial McGraw-Hill. (1992)