Funciones trigonométricas

Circunferencia trigonométrica: lo que tiene de especial es que su radio es igual a la unidad: r = 1.

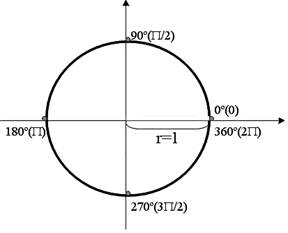
El ángulo de la circunferencia es 360º y la longitu de la misma está dada por “2pr” y como r = 1, long circ = 2p. (Ojo: la longitud de circunferencia siempre es 2 por

Para pasar del sexagesimal a radical, dividimos el sexagesimal (por ejemplo, 240º) por 180 y le agregamos p. Entonces, según el ejemplo, 240/180 = 4/3, o que sea 240º en radical es 4/3 p.

Para pasar de radical a sexagesimal, usamos el proceso inverso: multiplicamos nuestro radical (sigamos con 4/3 p) por 180º y nos da nuestro sexagesimal original: 240º.

(q: ángulo, p: número “pi”, irracional cuyo valor es 3,1415927......)

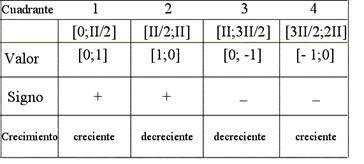
Función Seno

Sen q = y/r Es la “proyección” del radio vector sobre la ordenada (vertical)

Gráfica de la función seno

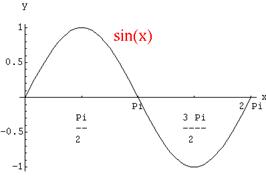
Dm = IR; Img = [-1; 1]; Período = 2p; Amplitud = 1

Recordemos que el período expresa cada cuánto se repite la misma curva hacia arriba y hacia abajo. Y la amplitud expresa qué oscilación tiene, cuánto sube o baja la curva. Ahh y acordate que el seno se “mide” en la ordenada.

Función coseno

Cos q = x/r Es la “proyección” del radio vector sobre la absi4sa (horizontal)

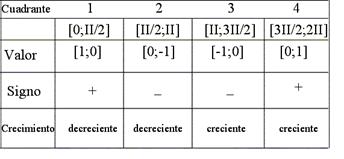
Gráfica de la función coseno

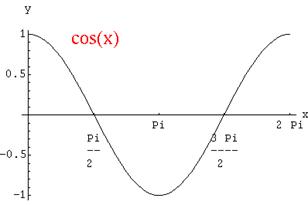
Dm = IR; Img = [-1; 1]; Período = 2p; Amplitud = 1

Veamos algunos indicios que nos da la misma fórmula. Damos los de la función sen pero los de cos son iguales:

y = asenx -›Img = [-a; a], A = a; P = 2p

y = sen(bx)-›Img = [-1; 1], A = 1; P = 2p/b

y = c+senx-›Img = [-1+c; 1+c], A = 1; P = 2p (si c es positivo, el desplazamiento es hacia arriba, si es negativo, hacia abajo)

y = sen(x- q)-›Img = [-1; 1], A = 1; P = 2p (si q es positivo, el desplazamiento es hacia la izquierda, si es negativo, a la derecha)

La imagen de las funciones trigonométricas:

Veámoslo a través de un ejemplo. Tomemos y = 3 + 2 sen(1/3 x). Entonces, sen(1/3 x) debe estar dentro del intervalo [-1; 1] (esto se mantiene siempre). Ahora vamos a ampliar el cálculo al segundo término (tomándolo entero) y para hacerlo multiplicamos el intervalo original [-1; 1] por 2. Tenemos entonces [-2; 2]. A ese resultado le sumamos el 3 del término que nos queda y tenemos que [1, 5] es la imagen de esta función

Reducciones al primer cuadrante:

La idea es encontrar el ángulo del segundo, tercero y cuarto cuadrante que tenga el mismo valor que el ángulo que tomemos del primer cuadrante.

Del primero al segundo: 180º - q (o, lo que es lo mismo, p - q)

Del primero al tercero: 180º + q (p + q)

Del primero al cuarto: 360º - q (2p - q)

Del segundo al primero: p - q

Del tercero al primero: q - p

Del cuarto al primero: 2p - q

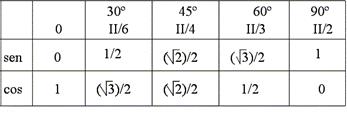
Valores más comunes de los ángulos del primer cuadrante

Gráficos de la función trigonométrica:

Tomemos, por ejemplo, y = senx+1/2. Lo igualamos a 0 y tenemos senx = -1/2. Nuestro número entonces es 1/2 (tomando su valor absoluto). Buscamos en nuestra tabla de valores del primer ángulo el que corresponde al sen y al número 1/2 y tenemos p/6. Ahora consideramos el signo y sabemos que el sen es negativo en los cuadrantes tres y cuatro. Usamos los pasajes de cuadrantes que vimos antes y así nos queda:

senx = -1/2

-› x = p +p/6 -› x = 7/6p +2kp (en el tercer cuadrante)

-›x = 2p - p/6 -› x = 11/6p +2kp (en el cuarto cuadrante)

(Aclaremos que 2kp se agrega siempre al final del cálculo como una forma de generalizar la cantidad de giros; k debe ser entero)

Por lo general el ejercicio nos va a plantear un intervalo al cual acotar nuestro cálculo. Supongamos que xE[-2p; 3p]. En ese caso debemos probar las k desde 0 (los valores que me dan con k = 0 representan al primer giro) y seguir con los valores correlativos. Lo mejor es empezar desde “un poco antes” del inicio del intervalo (en nuestro caso, un número anterior a -2) y terminar recién cuando la x me de algún número mayor que el final del intervalo (un número que pase 3p). (Si empezamos con -1 y ése ya pertenece al intervalo, conviene probar con -2 para evitar obviar algún x perteneciente al intervalo). Para calcular cada x debemos reemplazar cada k en ambas ecuaciones.

Damos un ejemplo de cálculo de x:

Tomamos k = -1 (que está dentro de nuestro intervalo), lo reemplazamos en nuestras ecuaciones y nos da:

x = 7/6p +2kp-› x = 7/6p +2(-1)p-› x = -5/6p (-0,83...p está dentro de nuestro intervalo así que esta x que encontramos será una de las raíces de la función)

x = 11/6p +2kp-› x = 11/6p +2(-1)p-› x = -1/6p (0,16... está dentro del intervalo así que x = -1/6p será otra raíz)

Este procedimiento se sigue hasta completar el cálculo de todas las raíces dentro del intervalo. Una vez que conseguimos eso, reemplazamos en la función por cualquier número de cada intervalo para x y calculamos la y correspondiente. Así sabremos si la curva “sube” o “baja” en esa parte de la función.(Si no estás familiarizado con este procedimiento podés verlo en la sección “función polinómica”). Si tenemos determinado un intervalo (como, en nuestro caso, [-2p; 3p]), la curva podrá ir desde la x = -2p a la x = 3p pero no más allá de esos valores (sería como trazar, al menos imaginariamente, AVx = -2p y AVx = 3p).

Las otras funciones trigonométricas:

Se definen en términos de las dos anteriores (sen y cos):

Tangente q = sen q / cos q = y/x

Cotangente q = cos q / sen q = 1/tan q

Secante q = 1 / cos q

Cosecante q = 1 / sen q