Movimiento circular
En esta sección vamos a definir las magnitudes
características de un movimiento circular, análogas a las ya definidas para el movimiento
rectilíneo.
Se define movimiento circular como aquél cuya
trayectoria es una circunferencia. Una vez situado el origen O de ángulos
describimos el movimiento circular mediante las siguientes magnitudes.
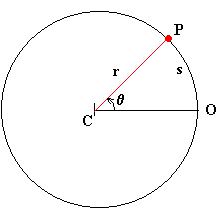
Posición angular, q
En el instante t el móvil se encuentra en el
punto P. Su posición angular viene dada por el ángulo q, que hace el
punto P, el centro de la circunferencia C y el origen de ángulos O.
El ángulo q, es el cociente entre la longitud
del arco s y el radio de la circunferencia r, q=s/r. La
posición angular es el cociente entre dos longitudes y por tanto, no tiene
dimensiones.
Velocidad angular, w
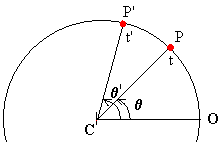
En el instante t' el móvil se
encontrará en la posición P' dada por el ángulo q '.
El móvil se habrá desplazado Dq=q ' -q en el intervalo de tiempo Dt=t'-t
comprendido entre t y t'.
Se denomina velocidad angular media al cociente entre
le desplazamiento y el tiempo.
![]()
Como ya se explicó en el movimiento rectilíneo, la
velocidad angular en un instante se obtiene calculando la velocidad angular
media en un intervalo de tiempo que tiende a cero.
![]()
Aceleración angular, a
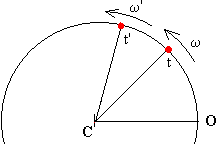
Si en el instante t la velocidad
angular del móvil es w y en el instante t' la velocidad angular
del móvil es w'. La velocidad angular del móvil ha cambiado Dw=w' -w
en el intervalo de tiempo Dt=t'-t comprendido entre t y t'.
Se denomina aceleración angular media al cociente
entre el cambio de velocidad angular y el intervalo de tiempo que tarda en
efectuar dicho cambio.
![]()
La aceleración angular en un instante, se obtiene
calculando la aceleración angular media en un intervalo de tiempo que tiende a
cero.
![]()
Dada la velocidad angular, hallar el desplazamiento
angular
Si conocemos un registro de la velocidad angular del
móvil podemos calcular su desplazamiento q -q0 entre los
instantes t0 y t, mediante la integral definida.
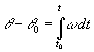
El producto w dt representa el desplazamiento
angular del móvil entre los instantes t y t+dt, o en el intervalo
dt. El desplazamiento total es la suma de los infinitos desplazamientos
angulares infinitesimales entre los instantes t0 y t.
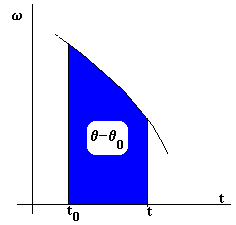
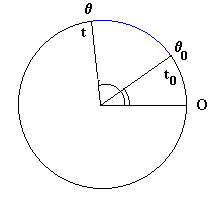
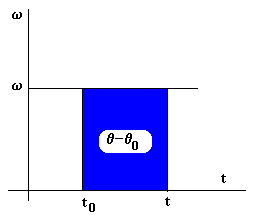
En la figura, se muestra una gráfica de la velocidad
angular en función del tiempo, el área en color azul mide el desplazamiento
angular total del móvil entre los instantes t0 y t, el
arco en color azul marcado en la circunferencia.
Hallamos la posición angular q del móvil en el
instante t, sumando la posición inicial q0 al
desplazamiento, calculado mediante la medida del área bajo la curva w-t
o mediante cálculo de la integral definida en la fórmula anterior.
Dada la aceleración angular, hallar el cambio de
velocidad angular
Del mismo modo que hemos calculado el desplazamiento
angular del móvil entre los instantes t0 y t, a partir
de un registro de la velocidad angular w en función del tiempo t,
podemos calcular el cambio de velocidad w -w0 que experimenta
el móvil entre dichos instantes, a partir de una gráfica de la aceleración
angular en función del tiempo.
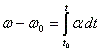
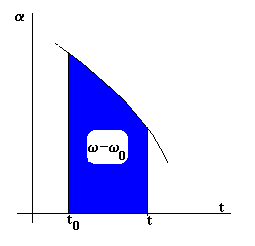
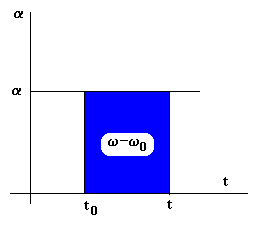
En la figura, el cambio de velocidad w -w0 es el área bajo la curva a - t, o el valor numérico de la integral definida en la fórmula anterior.
Conociendo el cambio de velocidad angular w -w0,
y el valor inicial w0 en el instante inicial t0,
podemos calcular la velocidad angular w en el instante t.
Resumiendo, las fórmulas empleadas para resolver
problemas de movimiento circular son similares a las del movimiento
rectilíneo.
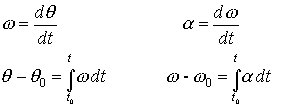
Movimiento circular uniforme
Un movimiento circular uniforme es aquél
cuya velocidad angular w es constante, por tanto, la aceleración angular
es cero. La posición angular q del móvil en el instante t lo
podemos calcular integrando
q -q0=w(t-t0)
o
gráficamente, en la representación de w en función de t.
Habitualmente, el instante inicial t0
se toma como cero. Las ecuaciones del movimiento circular uniforme son análogas
a las del movimiento
rectilíneo uniforme
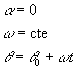
Movimiento circular uniformemente acelerado
Un movimiento circular uniformemente acelerado es aquél cuya aceleración a es constante.
Dada la aceleración angular podemos obtener el cambio
de velocidad angular w -w0 entre los instantes t0
y t, mediante integración, o gráficamente.
![]()
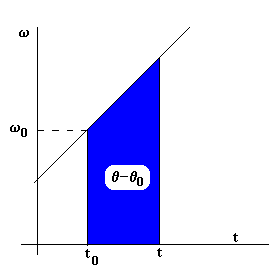
Dada la velocidad angular w en función del
tiempo, obtenemos el desplazamiento q -q0 del móvil entre los
instantes t0 y t, gráficamente (área de un rectángulo
+ área de un triángulo), o integrando
![]()
Habitualmente, el instante inicial t0
se toma como cero. Las fórmulas del movimiento circular uniformemente acelerado
son análogas a las del movimiento
rectilíneo uniformemente acelerado.
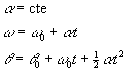
Despejando el tiempo t en la segunda ecuación y
sustituyéndola en la tercera, relacionamos la velocidad angular ω con el desplazamiento θ-θ0
![]()