Teorema del Seno
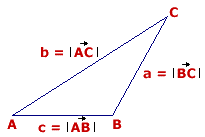
Existe una relación muy útil para la resolución de triángulos que relaciona los lados con los ángulos. Esta relación es conocida como teorema del seno
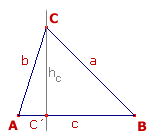
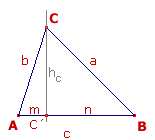
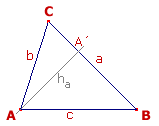
	En el triángulo AC´C se verifica de donde h c = b × sen(A) Análogamente en el triángulo BC´C y obtenemos h c = a × sen(B) Igualando ambas expresiones resulta la igualdad a × sen(B) = b × sen(A) expresión equivalente a Igualmente podemos considerar los triángulos rectágulos AA´C y ABA al trazar la altura relativa al vértice A. Mediante un razonamiento análogo al anterior obtendremos
De las expresiones obtenidas podemos deducir que expresión conocida como teorema del seno (o de los senos) y que demuestra que la relación que existe entre los lados de un triángulo y los senos opuestos es siempre la misma.

El teorema es válido para cualquier tipo de triágulo.
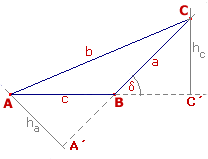
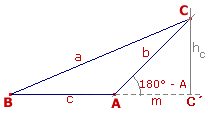
	En el triángulo obtusángulo de la figura si consideramos la altura h c relativa al vértice C, en el triángulo rectángulo AC´C resulta h c = b × sen(A) y en el triángulo rectángulo BC´C sen(δ) = sen(180 - B) = sen(B) = h c/a de donde h c = a × sen(B). Igualando ambas expresiones obtenemos Si consideramos la altura h a o bien h b y razonando de forma análoga obtenemos nuevamente la expresión del teorema.
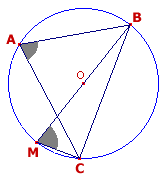
A partir del Teorema del Seno podemos relacionar fácilmente una triángulo con la circunferencia circunscrita al mismo. Si consideramos el triángulo ACB y es BM = d el diámetro de la circunferencia circunscrita, el triángulo BMC es recto en C y los ángulos A y M son iguales (pues abarcan el mismo arco BC). De todo ello resulta que sen(A) = sen(M) y como sen(M) = a/d Es decir, que en cualquier triángulo la relación entre un lado y el seno del ángulo opuesto es igual al diámetro de la circunferencia circunscrita a dicho triángulo.

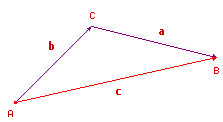
Una demostración vectorial del Teorema del Seno (En lo que sigue, las magnitudes vectoriales se designan en negrita) Efectuamos el producto vectorial AB × AC. Como AB = AC + CB y el producto vectorial es distributivo respecto a la suma de vectores, resulta AB × AC = (AC + CB) × AC = = AC × AC + CB × AC = CB × AC Repitiendo el mismo procedimiento, ahora teniendo en cuenta que AC = AB + BC AB × AC = AB × (AB + BC) = = AB × AB + AB × BC = AB × BC Es decir, los vectores AB × AC, CB × AC y AB × BC son iguales y por tanto tienen el mismo módulo | AB × AC | = | CB × AC | = | AB × BC | Como | AB × AC | = | AB | | AC | sen(A) = c b sen(A) | CB × AC | = | CB | | AC | sen(C) = a b sen(C) | AB × BC | = | AB | | BC | sen(B) = c a sen(B) es decir c b sen(A) = a b sen(C) = c a sen(B) y dividiendo esas igualdades por abc, se obtiene el teorema.

Teorema del Coseno
En el triángulo rectángulo AC´C se verifica b^2 = m^2 + hc^2 siendo m la proyección ortogonal del lado b sobre c y hc la altura relativa al vértice C.	Si m y n son las proyecciones ortogonales de los lados b y a sobre el lado c y consideramos el triángulo rectángulo BC´C resulta a^2 = hc^2 + n^2 = hc^2 + (c - m)^2 = = (hc^2 + m^2) + c^2 - 2cm = b^2 + c^2 - 2cm Expresión que proporciona el valor del cuadrado del lado opuesto a un ángulo agudo Como en el triángulo rectángulo AC´C es m = b×cos(A), si sustituimos en la expresión anterior a^2 = b^2 + c^2 - 2bc cos(A) Teorema del Coseno El cuadrado del lado opuesto a un ángulo agudo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de ellos por el coseno del ángulo comprendido.
En el triángulo rectángulo AC´C se verifica b^2 = m^2 + hc^2 siendo m la proyección ortogonal del lado b sobre c y hc la altura relativa al vértice C.		Sea el triángulo BAC obstusángulo en A. Si m es la proyección ortogonal del lado b sobre c tendremos a^2 = hc^2 + (c + m)^2 = c^2 + 2mc + (m^2 + hc^2) = = b^2 + c^2 + 2cm (*) Expresión que proporciona el valor del cuadrado del lado opuesto a un ángulo obtuso Como en el triángulo AC´C resulta que m = b cos(180 - A) = - b cos(A) si sustituimos en (*) volvemos a obtener la expresión obtenida anteriormente para el teorema del coseno. Es decir, dicho teorema se verifica para cualquier tipo de triángulo. (Para el caso particular que A = 90º obtendríamos el teorema de Pitágoras)
Tanto la expresión del cuadrado del lado opuesto a un ángulo agudo como la del cuadrado del lado opuesto a un ángulo obtuso son dos excelentes criterios para determinar con qué tipo de triángulo nos encontramos. Según que el cuadrado del lado de un triángulo sea menor, igual o mayor que la suma de los cuadrados de los otros dos, el ángulo seráa agudo, recto u obtuso. · Si los lado de un triángulo vinen dados por la terna (3,4,5) se trata de un triángulo rectángulo pues 3^2 + 4^2 = 5^2. · Si los lados vienen dado por la terna (3,5,7) se trata de un triángulo obtusángulo pues 3^2 + 5^2 = 34 < 7^2. · Si la terna de los lados es (7,8,10) el triángulo es acutángulo pues 7^2 + 8^2 = 113 > 10^2
			Una demostración vectorial del Teorema del Coseno Consiederemos un triángulo cualquiera ABC en el que a + b = c y las longitudes de los lados de dicho triángulo son los módulos de los vectores a, b y c. Multiplicando escalarmente a por sí mismo tenemos: aa = (c - b)(c - b) = bb + cc - 2 bc = = |b|^2 + |c|^2 - 2 |b||c| cos (b, c) Es decir |a|^2 = |b|^2 + |c|^2 - 2 |b||c| cos (b, c)