Vectores

Magnitudes físicas

· Magnitudes Escalares: un ejemplo de éstas es la masa. Para determinar la masa de una partícula es suficiente dar el valor de la misma y la unidad. Por ejemplo, 5 kg.

· Magnitudes Vectoriales: un ejemplo es la fuerza. Para determinar la fuerza que actúa sobre una partícula, además de dar el valor y la unidad, es necesario dar la dirección y el sentido de la misma. Por ejemplo, una fuerza de 4[N] en dirección vertical y sentido ascendente.

Así, una fuerza de 4[N] en la dirección EO, sentido hacia el O, se representa por una flecha cuya longitud (módulo) es de 4, orientada en la dirección y sentido indicado.

Definición:

Un vector es un segmento orientado en el espacio. Se puede caracterizar por:

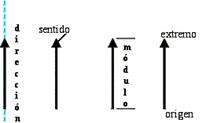
· Origen: a considerar cuando interese conocer el punto de aplicación del vector

· Dirección: o línea de acción coincidente con la de la recta que la contiene o cualquier otra recta paralela.

· Sentido: viene determinado por la punta de flecha localizada en el extremo del vector.

· Módulo: es la distancia entre el origen y el extremo del vector. Es la longitud del vector.

Acerca del vector posición y los versores

Cualquier objeto cuya posición pueda describirse localizando un solo punto puede llamarse partícula (no interesa su tamaño ni su estructura interna). Esta partícula puede moverse en una (recta), dos (plano) o tres (espacio) dimensiones. Podemos describir la posición de la partícula en un plano mediante: sus coordenadas cartesianas (R_x;R_y) o mediante un vector cuyo origen está en el centro de coordenadas.

El vector puede descomponerse (desdoblarse) en dos componentes (cada uno sobre un eje).

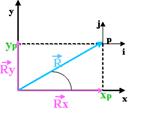
Cabe aclarar que x_p e y_p son son puntos que muestran “donde cae” la proyección del vector principal R. Pero los vectores R_x y R_y son las componentes de R sobre las abscisas y sobre las ordenadas respectivamente.

El vector posición se relaciona con sus componentes a través de las funciones trigonométricas del ángulo. Entonces:

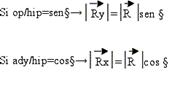
(Recordemos que el módulo indica la longitud del vector, ¡no puede ser negativo!)

Por otra parte, al resolver los cálculos anteriores, llegamos a ver que el módulo de cada componente es igual al valor de la coordenada correspondiente al eje donde se encuentra:

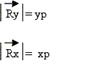
Los versores

Un vector puede nombrarse indicando el módulo de sus componentes y señalando sobre qué eje éstas se hallan. Para eso usamos los versores. El versor (o vector unitario) es un vector cuyo módulo siempre es uno.

Características de los versores:

· No tienen unidad

· Tienen módulo uno

se utilizan para expresar las direcciones de los vectores

En nuestro ejemplo, sobre el eje x encontramos al versor “i” y sobre el eje y hallamos el versor “j”. Entonces, podemos escribir al vector posición así:

Operaciones con vectores:

Sea o el origen...

Suma de vectores: sea oA = (3,5) y oB = (5,-7), entonces oA-oB = (8,-2) (es conmutativa)

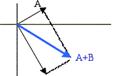
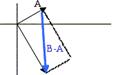
Resta de vectores: oA = (3,5) y oB = (5,-7), entonces B-A = (2,-12) (no es conmutativa porque si hubiera hecho A-B me habría dado el mismo vector pero con sentido opuesto)

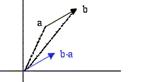
Pasaje al origen: si tengo ab y lo quiero pasar al origen (quiero que salga del 0) hago: ab = ob-oa, con lo cual ab = b-a, entonces

Multiplicación de un vector por un escalar: sea el vector (3, -1), multiplicado por k = 5, es simplemente (15, -5). Consecuencias de multiplicar unn vector por un escalar: si k es negativo, cambia el sentido del vector; si k es mayor que 1, “alarga” o “estira” el vector. Si es menor, lo acorta.

Vectores equivalentes: dos vectores son equivalentes si están aplicados en distintos puntos del espacio pero tienen igual dirección, sentido y módulo. Dos vectores son equivalentes si sus coordenadas son iguales. Así que si sabemos que (9x-2, 2x-1-3x) y (1, -4/3) son equivalentes, entonces calculo x sabiendo que 9x-2 = 1 y 2x-1-3x = -4/3

Punto medio: se calcula con la fómula M = (A + B)/2 y la idea sería uuna cosa así:

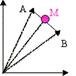
Norma de un vector (Módulo): es la distancia del punto al oriden y está dada por:

Producto escalar: se ve bien con un ejemplo (1, 2 , 3).(-1, 5, 0) = 1.(-1) + 2.5 + 3.0 = 9 (fijate que el resultado del producto escalar, que no es lo mismo que el producto por un escalar, tiene por resultado un escalar)

Relación del coseno:

lo cual nos lleva a decir quer dos vectores son perpendiculares cuando A.B = 0

Distancia entre dos puntos: d(A,B) = ||AB|| = ||B-A|| = ||A-B||