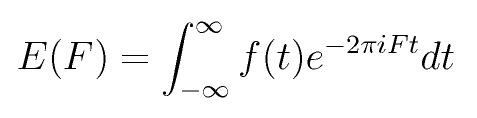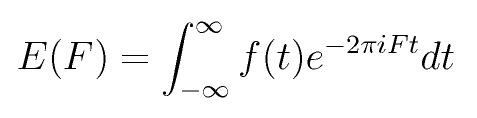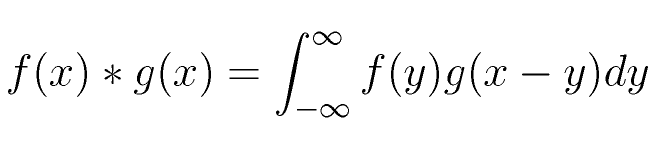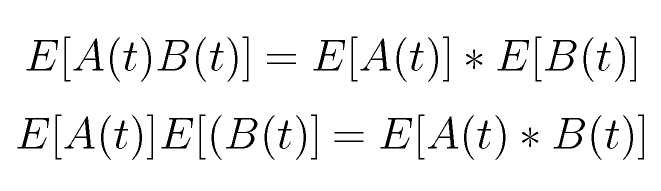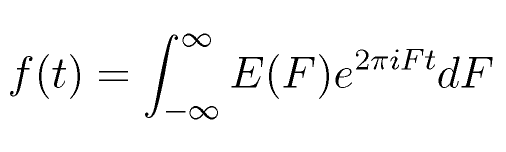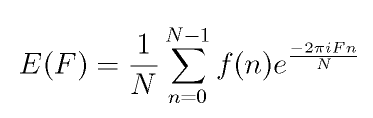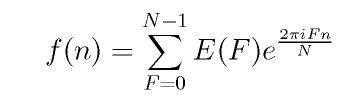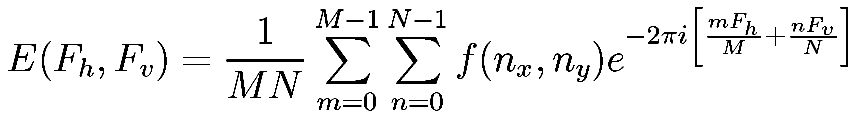El espacio de frecuencias
De dónde proviene, o cómo se puede obtener el espectro de amplitud
de una señal? La transformada de Fourier nos permite obtener
la representación de una señal en el espacio de frecuencias.
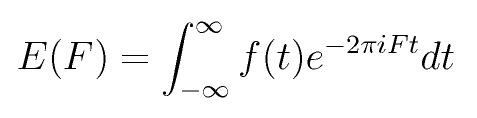
F representa cada una de las frecuencias que posiblemente contiene
la señal f(t).
La transformada de Fourier posee numerosas propiedades matemáticas importantes.
Modelo frecuencial de una señal muestreada
La señal muestreada puede pensarse como el producto de la señal contínua por
una función de muestreo (tren de impulsos). En determinadas condiciones,
el espectro de una señal muestreada consiste en copias periódicas del
espectro de la señal original.
Para ello, la señal original debe estar limitada en banda (contener
frecuencias solo por debajo de una frecuencia máxima), y la frecuencia de
muestreo debe ser mayor del doble de la frecuencia máxima (frecuencia de
Nyquist).
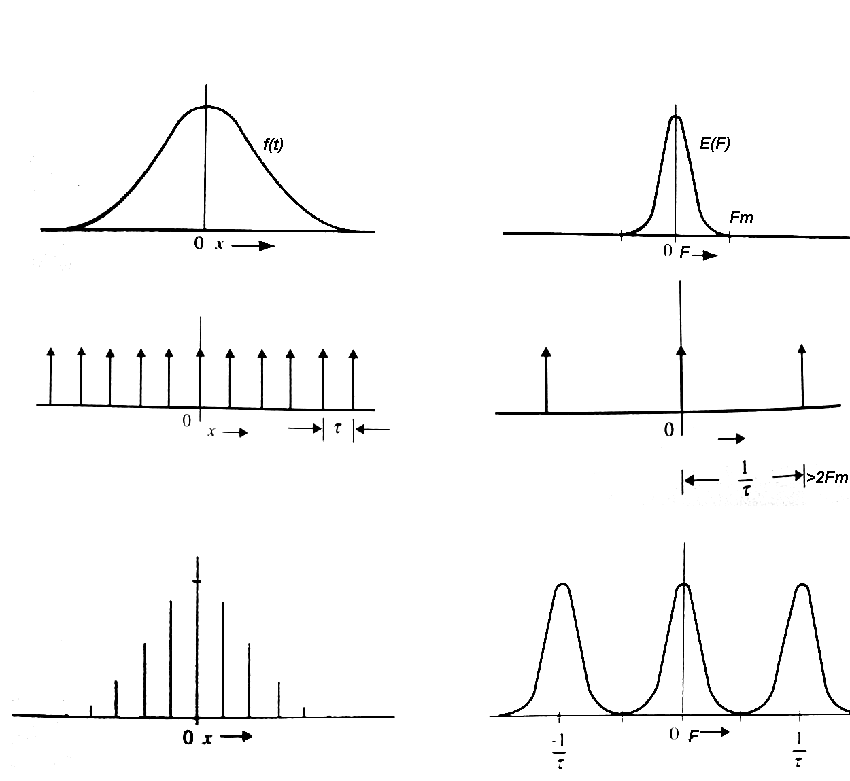
Espectro de una señal limitada en banda, muestreada por encima de la
frecuencia de Nyquist
Cómo puede obtenerse una expresión para el espectro de la señal muestreada?
Para ello se requiere el operador de convolución.
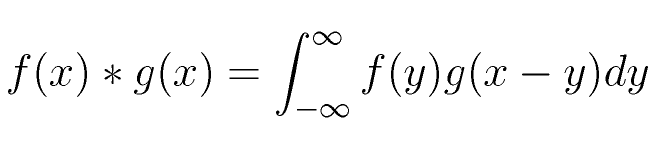
Definición de la convolución entre dos funciones

Ejemplo de convolución entre dos funciones
La convolucíon es la función dual del producto bajo transformada de Fourier,
es decir, dadas dos señales A(t) y B(t), y sus respectivos espectros E[A] y E[B],
entonces vale
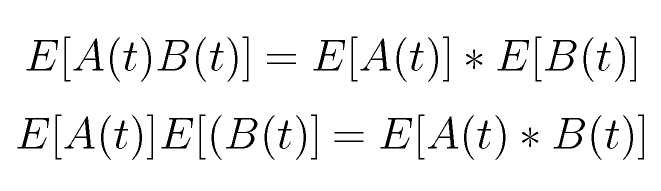
Este resultado nos permite pensar en manipular cualidades de la señal, alterando su
espectro.
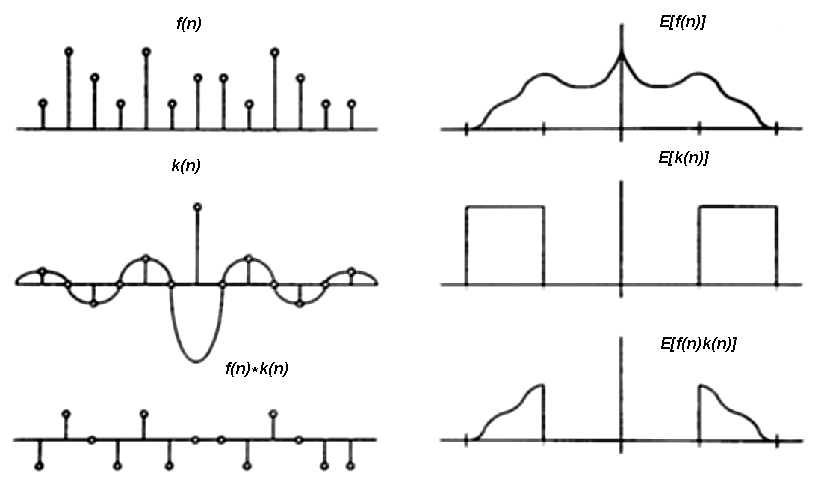
Filtrado pasaaltos de una señal discreta
La relación que nos permite obtener la señal discreta nuevamente a partir de su espectro,
es la transformada inversa de Fourier
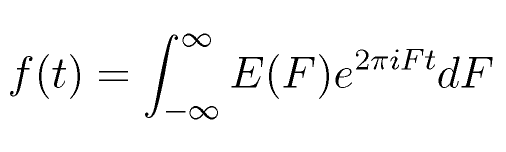
Podemos ahora encontrar una explicación para el proceso destructivo (aliasing) en el
muestreo. Simplemente, si no se cumple la condición de limitación en banda, parte del
espectro alto de cada copia replicada se "trasvasa" al espectro bajo de las copias
vecinas, lo cual es después imposible de filtrar.
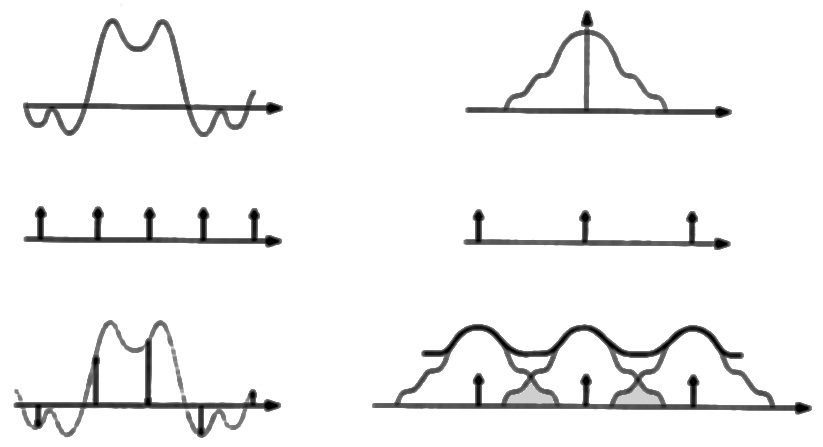
Aliasing en el muestreo inadecuado de una función
Transformada de Fourier discreta (DFT) y rápida (FFT)
La transformada de señales discretas y periódicas puede computarse con un algoritmo
numérico, la transformada de Fourier discreta, dado que la expresión "colapsa"
a una sumatoria.
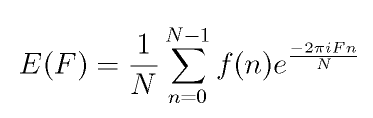
Transformada de Fourier discreta
El espectro de una función discreta y periódica, es también una función discreta
y periódica, y la señal original puede recobrarse con la transformada discreta
inversa.
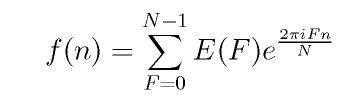
Transformada discreta inversa
Estas expresiones (cuya evaluación de complejidad cuadrática) pueden evaluarse
numéricamente por medio de algoritmos que aprovechan las simetrías de la
exponenciación. Así surge la FFT directa e inversa, de complejidad semicuadrática.
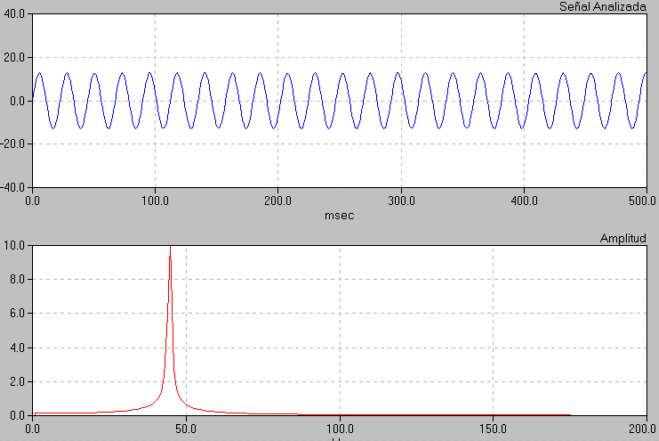
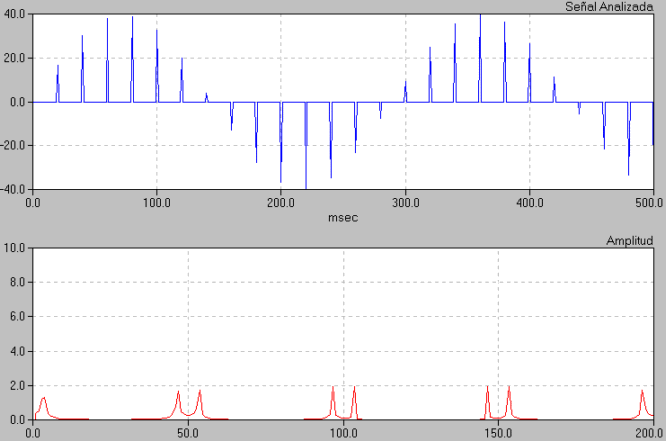
Aplicación que implementa la FFT
Transformada de Fourier discreta bidimensional
Siendo la transformada de Fourier un operador lineal y separable
(así como su versión discreta e inversa), entonces la TF discreta bidimensional
es
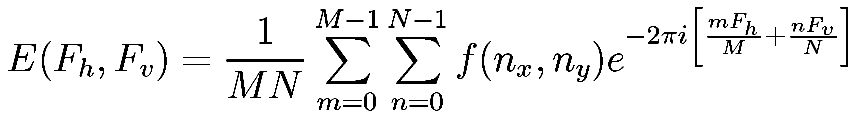
Por cuestiones de simetría y facilidad de interpretación, la representación
del espectro de una imágen se hace con una traslación periódica, de manera que
el (0,0) en frecuencias quede en el centro del espectro.
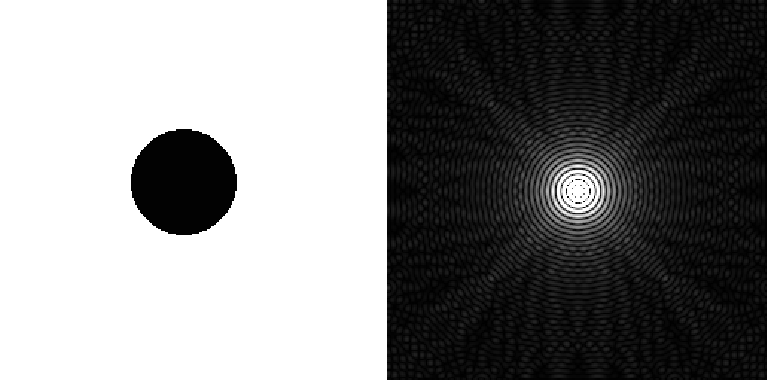
Una imagen y su transformada de Fourier

Interpretación de la TF de una imagen