Percepción y atributos visuales
Atributos visuales innatos (brillo ~> valor) y culturales (rojo ~> peligro).
Atributos visuales posicionales, temporales, y retinianos (tamaño, textura, orientación forma, transparencia, color).
Cómo se combinan, cuáles son más eficaces?
Procesamiento preatentivo
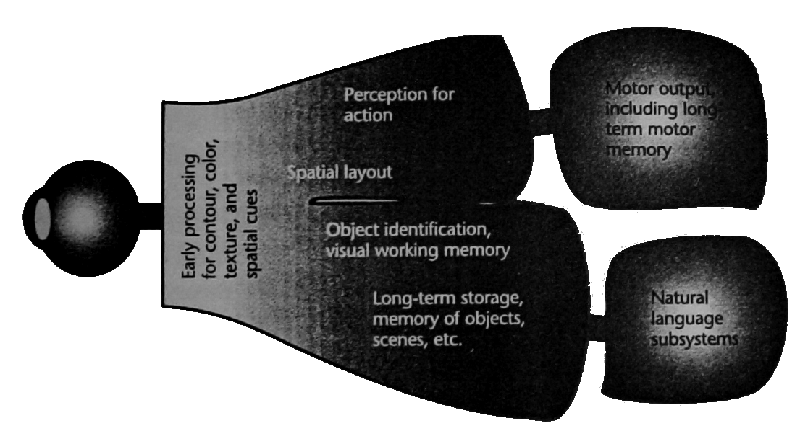
Algunos atributos

Un ejemplo: contar cuántos "3" hay

Texturas

Un ejemplo: percepción tridimensional
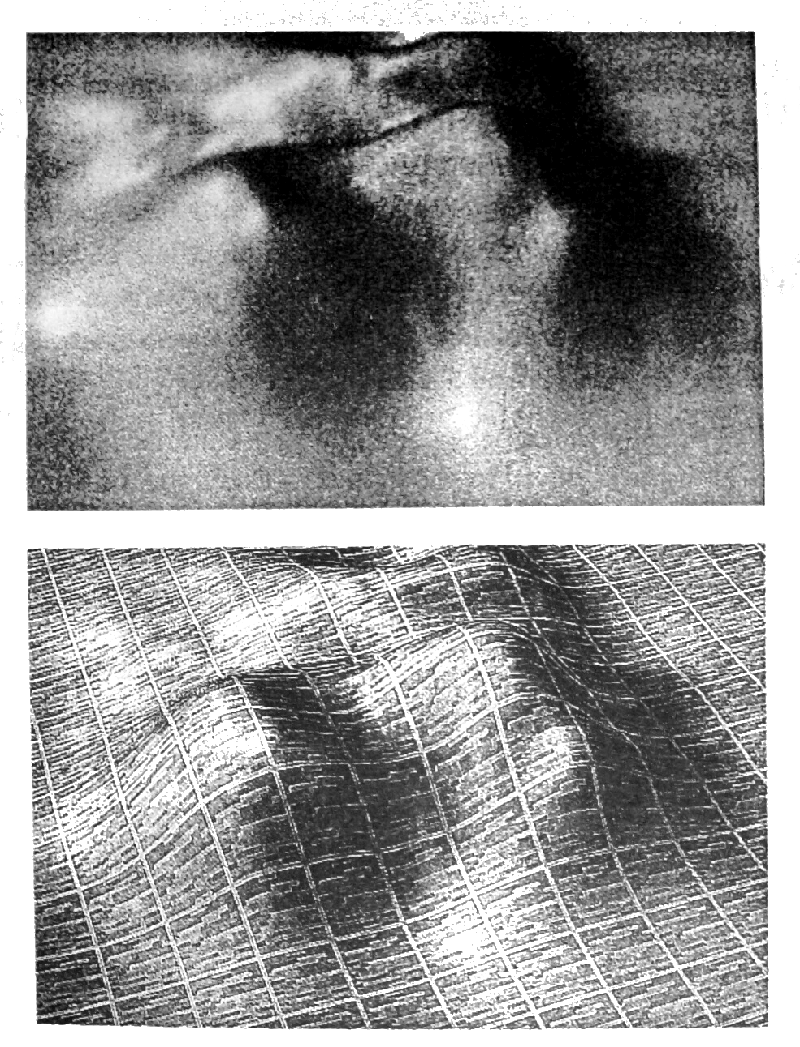
Saturación ~> datos ordinales.
Luminancia ~> datos cuantitativos y ordinales. (Obs.: la disminución de la luminancia puede producir efecto de profundidad.)
Textura ~> datos nominales. (Obs.: cuidado con texturas superpuestas; las texturas pueden producir efecto de densidad.)
Orientación ~> Poco adecuada. Utilizar siempre con formas conocidas. Respecto del eje vertical.
Profundidad ~> 3D. Disminuir el brillo mejora la percepción de profundidad. Técnicas de la CG: perspectiva, cara oculta, transparencia.
| Cuantitativos | Ordinales | Nominales | |
|---|---|---|---|
| Posición | + | + | + |
| Tamaño (absoluto) |
+ | + | + |
| Orientación (relativo) |
0 | 0 | + |
| Escala de grises (diferencias) |
+ | + | - |
| Escala de grises (absoluto) |
- | + | - |
| Paleta arco iris (diferencias) |
0 | + | + |
| Paleta arco iris (absoluto) |
- | - | + |
| Forma (diferencias o absoluto) |
- | - | + |
| Textura (diferencias o absoluto) |
0 | 0 | + |
Proximidad (los objetos más próximos tienden a percibirse como una unidad).
Similitud (los objetos similares tienden a percibirse como una unidad).
Clausura (los contornos y fronteras próximos tienden a unirse).
Continuación (los segmentos de recta, arcos de circunsferencia y otras formas simples tienden a continuarse).
Organización en figura-fondo.
Curvas de nivel. Difícil captación de valores cuantitativos, determinar mínimos o máximos locales, establecer comparaciones. Son adecuados para visualizar los lineamientos de una distribución (pendientes, cortes).
Superficies. Adecuadas para geometrís o formas reconocibles. Es conveniente mejorar la percepción tridimensional con otras pautas (shading, sobreimponer una textura uniforme).
Datos volumétricos. Agregar superficies isopotenciales por medio de transparencias. Utilizar planos de corte.
Texturas: Percepción, modelos matemáticos y síntesis.

Modelo de Gabor
Se basa en tres parámetros: Orientación, Frecuencia y Posición.
T ~> cos(OF)exp(-PF)

Según este modelo, la segmentación (separación perceptual) de zonas con diferente textura se realiza identificando áreas cuyo ajuste con el modelo de Gabor sea similar.
Una señal periódica puede modelarse matemáticamente como una sumatoria de señales periódicas simples. En el caso de las series de Fourier se utilizan las funciones senoidales como base.
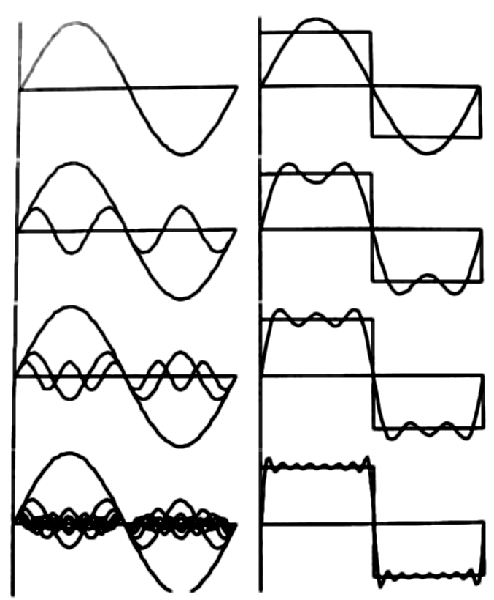
Ejemplo de serie de Fourier para una señal periódica rectangular
El teorema de Fourier muestra que una señal periódica f(t) puede representarse con una serie
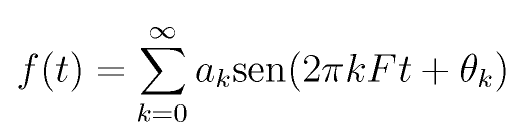
donde cada factor a de amplitud de cada término de la serie determina el espectro de amplitud de la señal original, y F es la frecuencia fundamental de la señal.
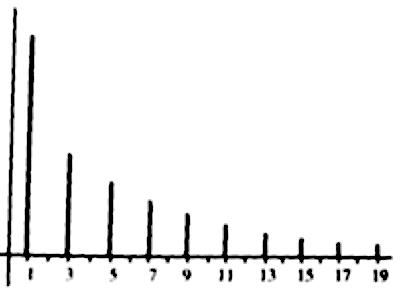
Espectro de amplitud de la señal periódica rectangular
De dónde proviene, o cómo se puede obtener el espectro de amplitud de una señal? La transformada de Fourier nos permite obtener la representación de una señal en el espacio de frecuencias.
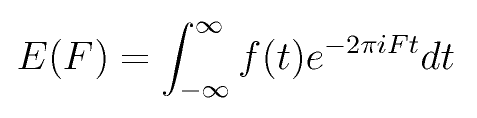
F representa cada una de las frecuencias que posiblemente contiene la señal f(t).
La transformada de señales discretas y periódicas puede computarse con un algoritmo numérico, la transformada de Fourier discreta, dado que la expresión "colapsa" a una sumatoria.
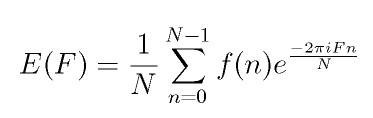
Transformada de Fourier discreta
El espectro de una función discreta y periódica, es también una función discreta y periódica, y la señal original puede recobrarse con la transformada discreta inversa.
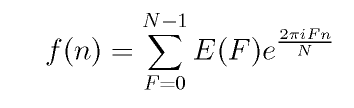
Transformada discreta inversa
Estas expresiones (cuya evaluación de complejidad cuadrática) pueden evaluarse numéricamente por medio de algoritmos que aprovechan las simetrías de la exponenciación. Así surge la FFT directa e inversa, de complejidad semicuadrática.
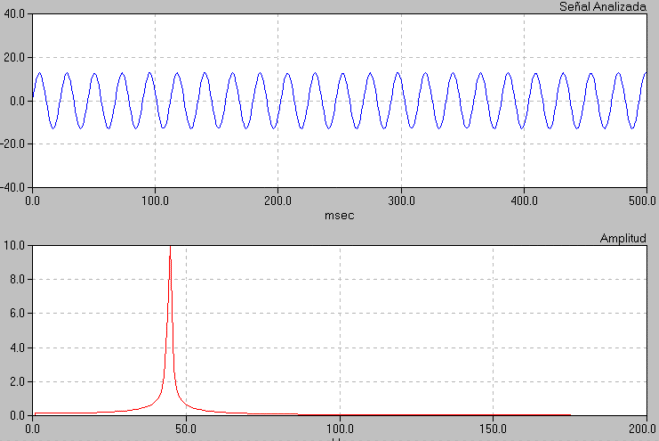
Aplicación que implementa la FFT
Siendo la transformada de Fourier un operador lineal y separable (así como su versión discreta e inversa), entonces la TF discreta bidimensional es
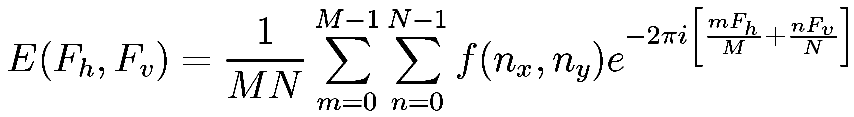
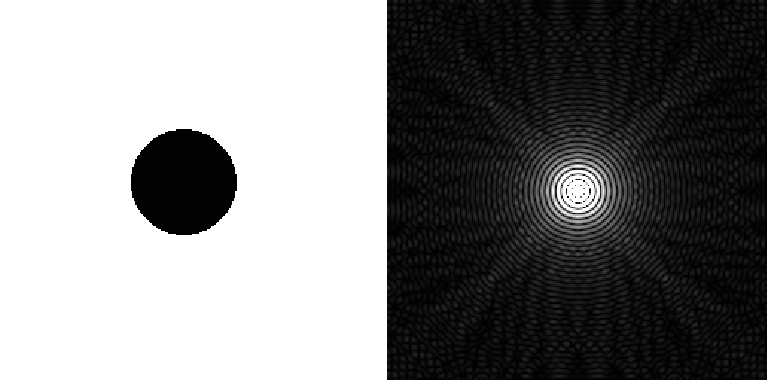
Una imagen y su transformada de Fourier

Interpretación de la TF de una imagen
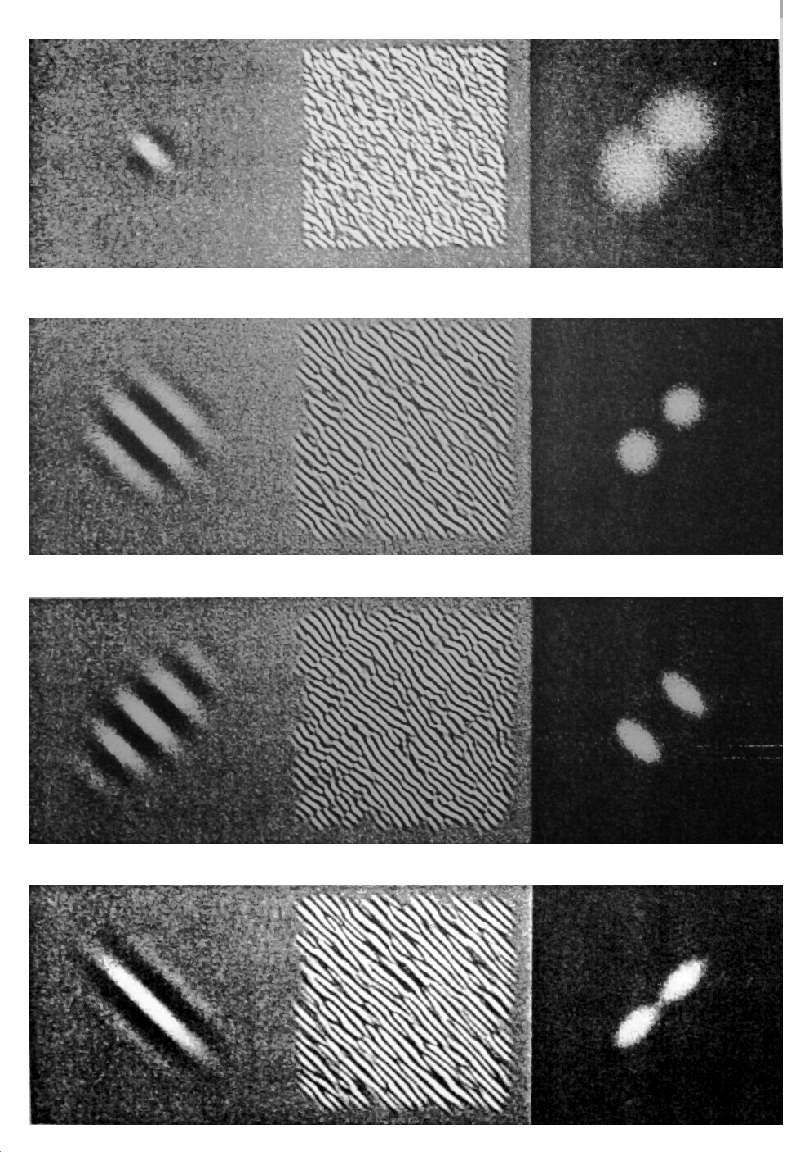
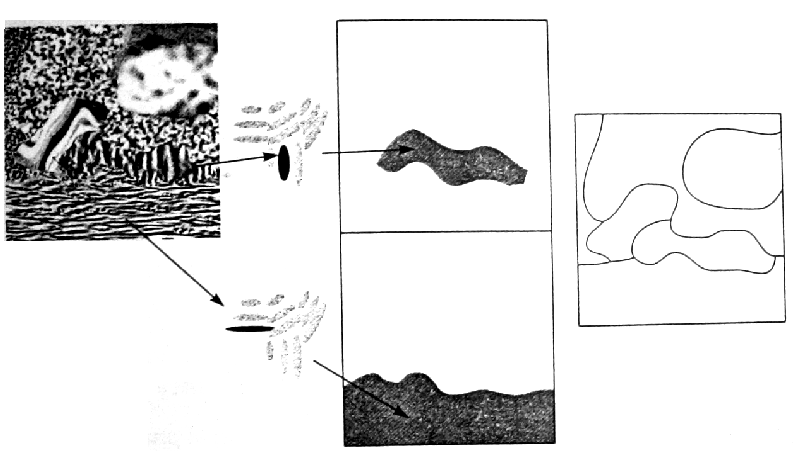
Elementos del modelo de Gabor (izq.), agregados aleatóriamente en una imagen (centro), y transformada de Fourier del resultado (der.)
Los parámetros de textura de Gabor son adecuados para representar aisladamente valores ordinales o cuantitativos, pero su contraste es diferente en cada caso:

Al mismo tiempo, es importante observar la existencia de fenómenos análogos al contraste simultáneo de luminancia:

La idea consiste en utilizar los valores diferenciales locales de una superficie para determinar los parámetros de la textura.
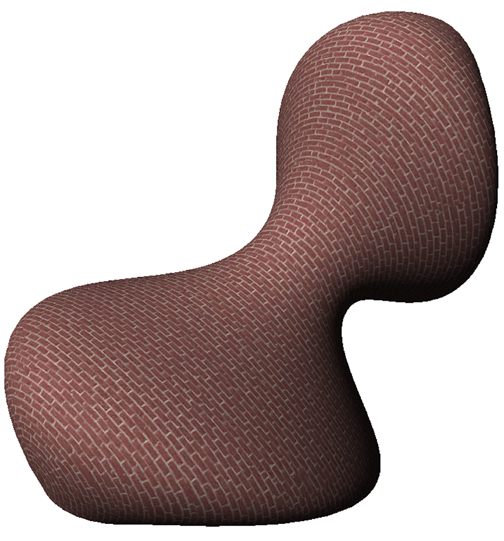
La textura se acomoda según una dirección constante.
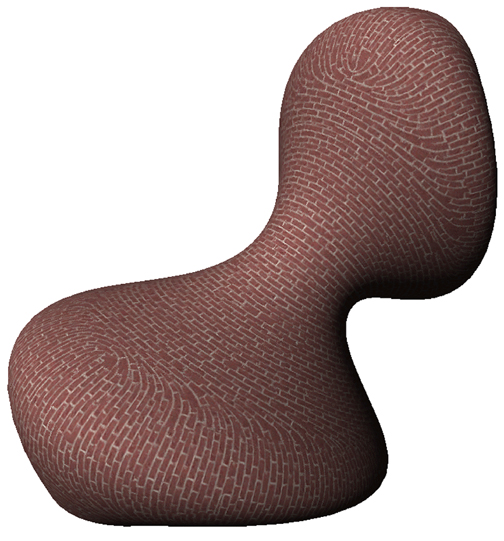
La textura se acomoda según la dirección del mayor gradiente de curvatura.
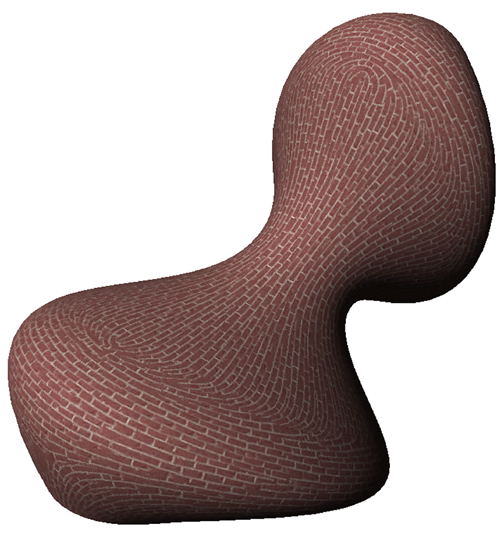
La textura se acomoda según la dirección del menor gradiente de curvatura.
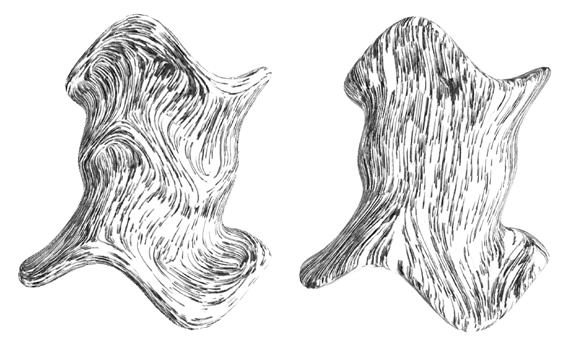
Menor gradiente de curvatura vs. dirección constante.

Superficie con modelo de iluminación.

Tres texturas (1D, 2D y LIC).

Textura 1D, orientada según dirección del máximo gradiente.

Textura LIC, orientada según dirección del máximo gradiente.

Textura 2D, orientada según dirección del gradiente.
En los experimtentos, se muestra que esta última textura es la que minimiza el error en la percepción local de la forma de la superficie.
Percepción de forma 3D en superficies transparentes.

Superficie transparente sin y con textura.
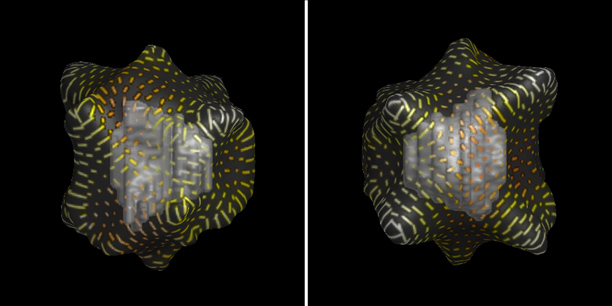
Textura que codifica magnitudes diferenciales en la superficie.
