Representación y Rendering de Volúmenes
(Agradecemos a Andrea Silvetti por facilitarnos el material necesario para esta parte de la presentación.)
Buscar un entendimiento global de determinadas propiedades de los datos.
Innumerable cantidad de aplicaciones.
- Construcción de un MODELO EMPÍRICO.
- Construcción de un MODELO ABSTRACTO.
- Construcción de un MODELO VISUALIZADO.

Realimentación para ajustar parámetros y
lograr mayor insight sobre los datos.

Los datos crudos pasan por una serie de procesos resultando en datos derivados.
Ejemplos de esos procesos:
- Interpolación: para obtener valores faltantes
cuando la información es incompleta.
- Transformación de coordenadas: si los datos
se procesan y visualizan mejor en un sistema de coordenadas
alternativo.
- Normalización: para llevar los datos a un
rango de valores predefinidos.

A partir de los datos derivados se crea el objeto de visualización abstracto.
Ejemplos:
- Asignación de color y opacidad a partir de
una función transferencia aplicada
a valores escalares de un volumen.
- Extracción de una superficie a partir de
un valor umbral.
La elecciónn correcta de la función transferencia es difícil, y debe ser adecuada para obtener un buen insight sobre los datos.
Ejemplo: la tabla de color para visualizar una tomografía, debería proyectar valores de densidad de huesos a blanco/opaco, de músculos a rojo/semitransparente, y de tejido graso a amarillo/muy transparente.

Se convierte la representación computacional de los datos en una imagen visual, mediante un proceso denominado rendering.
Ejemplos:
- Elección de los parámetros de visión:
punto de vista, tipo de proyección (paralela o perspectiva),
etc.
- Viewing: determinación de lo que debe verse
a través de cada pixel en la pantalla.
- Shading: simulación de la interacción
de la luz para determinar el color final para cada pixel
de la imagen.
- Sensores (tomógrafos, satélites).
- Tareas computacionales (simulaciones o análisis
por elemento finito).
- Muestreos y mediciones.
Son un conjunto de muestras V(x,y,z)=v donde:
- (x,y,z): es una posición 3D.
- v escalar: representando una propiedad medible en (x,y,z).
- v multivaluado: si representa simultáneamente
varios datos.
Se pueden calcular muestras intermedias (remuestreo):
- Por medio de interpolación constante (toma
el valor del vecino más cercano).
- Por medio de interpolación bilineal o trilineal.
- Voxels: cuando la interpolación es constante.
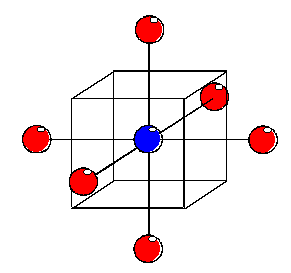
Un voxel es un área hexaédrica alrededor de un punto de grilla con valor constante igual al valor de dicho punto. - Celdas: cuando la interpolación es de mayor orden.
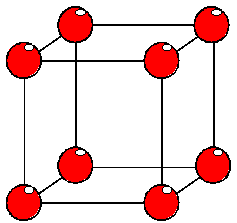
Una celda es un área hexaédrica cuyas esquinas son puntos de grilla y los valores varían entre dichos puntos.
Grilla tetraédricas: todos sus elementos son tetraedros sin conectividad explícita. No hay restricción en cuanto al número de arcos que llegan a un vértice.
Grilla cuberrilla: grillas regulares ralas que se completan interpolando o aproximando los datos ralos bajo modelos matemáticos definidos sobre todo el dominio.
Modelos locales (Simples pero menos reales).
- Sólo consideran la interacción
entre los iluminantes y los objetos.
- La información de profundidad sólo permite
indicar la forma de los objetos.
- Los objetos pueden actuar como fuentes de luz.
- Consideran la luz reflejada entre objetos.
- Introducen la noción de la distancia tridimensional
en la imagen.
Modelos globales para superficies:
- Consideran un medio de refracción homogénea
entre superficies que no participa de la
disipación de la luz.
- Modelos usuales en Computación Gráfica (Ray
tracing, Radiosidad, ecuación del rendering, métodos
de dos pasadas combinando ray tracing y radiosidad).
- Se utilizan:
- Ray tracing.
- Radiosidad.
- La ecuación del rendering.
- Métodos de dos pasadas combinando ray tracing y
radiosidad.
- Ray tracing.
- Consideran al volumen como un medio participante
que puede absorber, disipar, emitir y refractar
la luz que fluye a través.
- Esto es lo que hace que la Visualización sea
una disciplina aparte de la Computación Gráfica.
- Se utilizan:
- Ray tracing volumétrico.
- Radiosidad volumétrica.
- La ecuación del rendering y su
simplificación.
- Composición volumétrica
(para evaluar la ecuación del rendering).
- Ray tracing volumétrico.
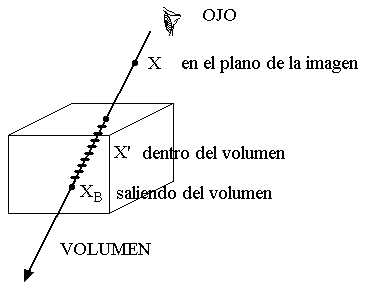

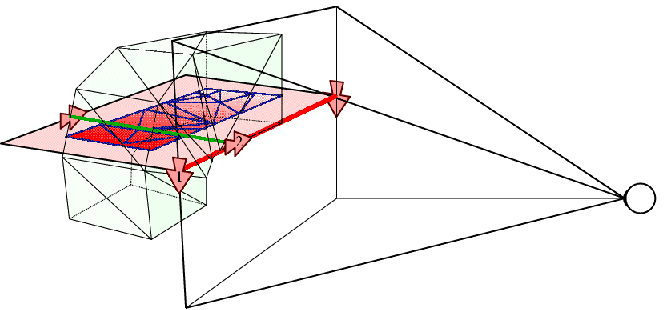
Calcula la intensidad en cada pixel x de la imagen integrando a lo largo del rayo de visión las intensidades de cada punto x', atenuadas por la dispersión de la luz antes de alcanar el ojo (entre x y x'). r(x'') corresponde a la densidad del sólido en el punto x''.
- La intensidad de la luz es atenuada por los objetos en
forma proporcional a la intensidad de energía que
estos reciben.
- El objeto en sí mismo puede emitir luz con una
cierta intensidad.
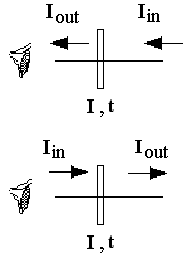
La composición puede hacerse de dos formas con igual resultado:
|  |
|
Combina la intensidad Ii del i-ésimo elemento,
su transparencia ti y la intensidad entrante Ii-in
para obtener la intensidad saliente Ii-out.
| 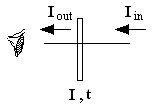 |
La intensidad Fi acumulada hasta el paso i es:
Fi = ti * Fi-1 + Ii
La forma de computar la intensidad final en un rayo es:
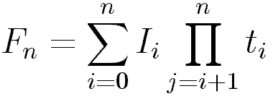
La composición front-to back puede resolverse
de manera similar.
Rendering de Superficies: técnicas que primero convierten los datos a una representación intermedia, que en general es una superficie exterior o umbral del volumen.
Rendering Directo de Volúmenes (DVR): técnicas que visualizan directamente al conjunto de datos sin pasar por representaciones intermedias.
No pasan a una representaciones de superficies, ni se visualizan de manera directa.
Grafican dominios 3D usando técnicas convencionales de computación gráfica.
Generalmente, trabajan con los datos sobre una grilla cuberrilla (datos ralos).
Algunos métodos interactivos para datos geométricos:
- Contornos de Wireframe (líneas).
- Tiny Cubes (cubos o esferas de tamaño variable
sin transparencia).
- Vanishing cubes (lados de celdas proyectados
con transparencia).

- Slicing (superpone capas del volumen con transparencia).
- Métodos interactivos para datos valuados:
Brushing (resolución variable con transparencia). - Cualitativo (clasificación por valor umbral).
- Planar (cortes transversales).
- Cualitativo (clasificación por valor umbral).
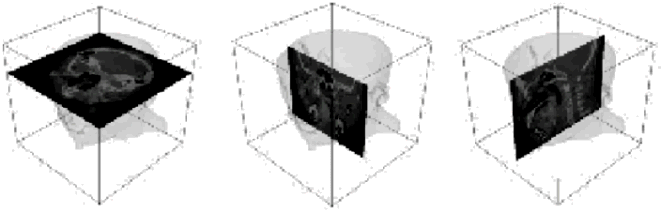
- Volumétrico (identificación de un
subvolumen).
Son rápidos y sencillos.
Aprovechan el hecho que los métodos para mostrar primitivas geométricas están bien establecidos, ya sea por software o por el uso de hardware de aceleración.
Transmiten menos información.
Se pierde una dimensión de información y no sirven para visualizar conjuntos de datos con formas complejas.
Los pasos básicos de cualquier algoritmo de este tipo son:
- Extraer la superficie a partir de una valor umbral.
- Elegir parámetros de visión, de
iluminación, tipo de proyección, etc.
- Renderizar las primitivas geométricas.
Algunos métodos de superficies destacados.
- Cubos opacos: Renderiza un cubo opaco en cada celda
cuyo valor está debajo del umbral.
Es muy notoria la formación de bloques.
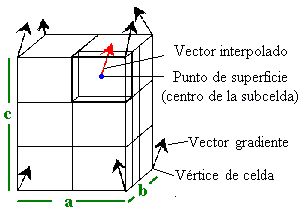
- Dividing Cubes: Renderizan puntos 3D basado en celdas.
Divide adaptativamente las celdas hasta lograr proyecciones
puntuales.
- Tracking de contornos: Conecta isocontornos en cortes
transversales, produciendo un conjunto de triángulos
que son renderizados por librería.
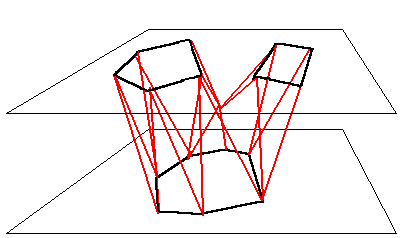
- Tracking de isosuperficies: Extrae una superficie
umbral como conjunto de triángulos, que luego son
renderizados por librería.
Son muy utilizados porque se adaptan bien a datos estructurados en celdas o a datos tetraedrizados (estructuras menos restringidas y más frecuentes).
El primero de los casos se denomina marching cubes.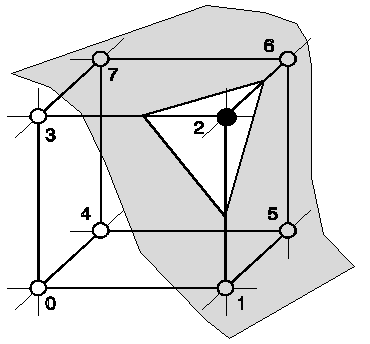
Clasifica cada celda según los valores de sus vértices respecto al valor umbral.
Una celda pertenece a la superficie si tiene al menos un vértice con valor inferior al umbral y otro con valor superior a éste.
Son posibles 2^8 = 256 combinaciones de celdas de superficie, que se reducen a 128 por complemento y a 15 por rotaciones.
Equivalencia por complemento: Invertir los puntos marcados y luego invertir los normales de los triángulos.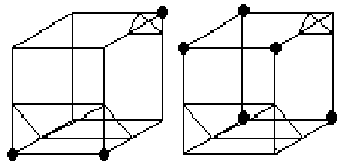
Equivalencia por rotación.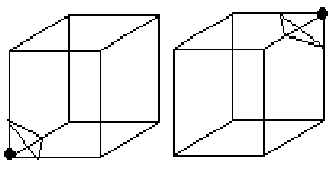
15 configuraciones originalmente propuestas.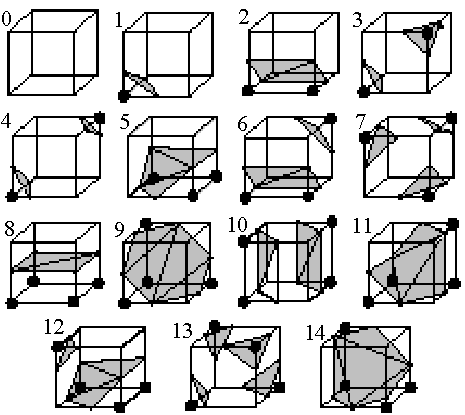
Problema: El algoritmo original produce superficies con "agujeros" cuando dos celdas adyacentes comparten una cara que es considerada de manera diferente en cada caso.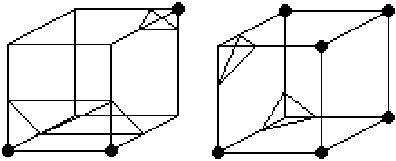
El segundo de los métodos de tracking de isosuperficies se denomina marching tetrahedra.
En la siguiente figura hay que considerar solamente los primeros tres casos, los otros tienen en cuenta la posibilidad de que el valor de la celda coincida con el umbral (vértices marcados en gris).
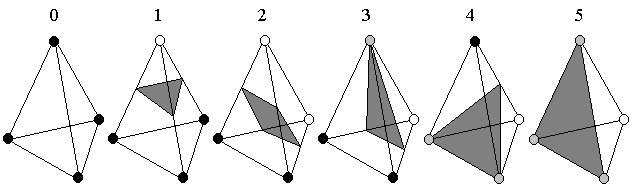
Transmiten más información que las otras técnicas.
Involucran el uso de modelos de iluminación más elaborados (transparencia, absorción, difusión, etc.).
Algoritmos son más complejos, y en consecuencia más lentos.
No convierten los datos a una representación intermedia, por lo que son apropiados para datos no estructurados, o cuya forma es geométricamente compleja.
Los pasos básicos de cualquier algoritmo DVR son:
- Asignar un color y una opacidad a cada
muestra de datos (función transferencia).
- Proyectar las muestras sobre el plano de la imagen.
- Mezclar las proyecciones en base a un modelo físico
de propagación de la luz sobre un material
semitransparente y coloreado.
Se dividen en algoritmos de:
- Forward mapping: mapean los datos sobre la
imagen.
- Backward mapping: mapean el plano de la imagen
sobre los datos.
Recorren los pixels en el espacio de la imagen determinando la contribución de los datos visibles desde cada pixel por los siguientes caminos:
- Por trazado de rayos.
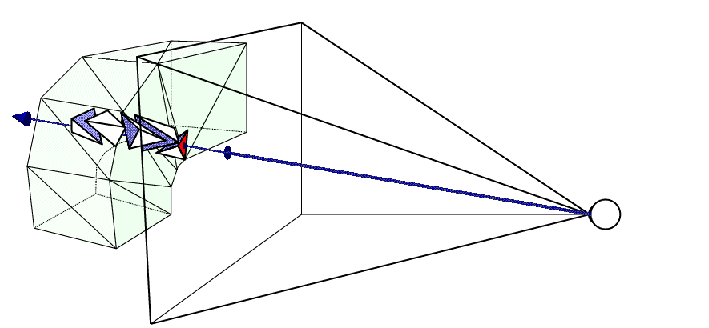
- Mediante líneas de barrido.
- Mediante líneas de barrido.
Paralelizables a nivel de rayos (datos repetidos en cada nodo).
Generan cada muestra de salida a partir de varias de entrada.
En general usan interpolación como kernel de reconstrucción y por lo tanto suelen precisar técnicas de anti-aliasing.
- Métodos que simulan el transporte de luz.
Muy buena calidad en imágenes luminosas pero lentos. Modelan el fenómeno de transporte de luz que simula la ecuación del rendering. Evaluan la integral que simula la luz proveniente de objetos traslúcidos.
- Ray Casting (trazado de rayos que atraviesan
el volumen calculando la contribución en cada paso).
Ray Casting basado en voxels: (interpolación constante, luego tiene la ventaja de mayor simplicitad, velocidad, y la desventaja de mayor aliasing por discretización de rayos).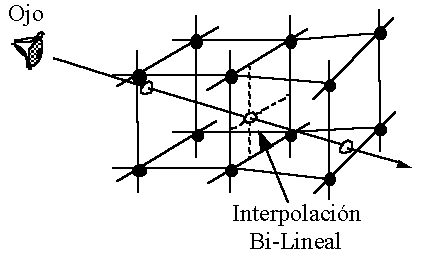
Puede evaluarse por medio de un rayo contínuo (como en el ray tracing de computación gráfica), o por medio de rayos discretos (trazado de rayos generados por algoritmos de línea tipo DDA 3D).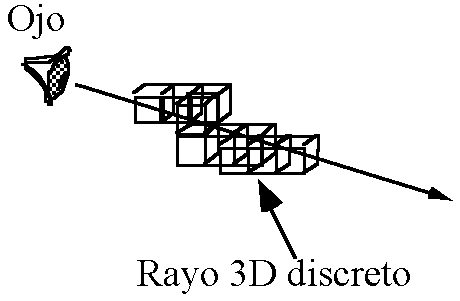
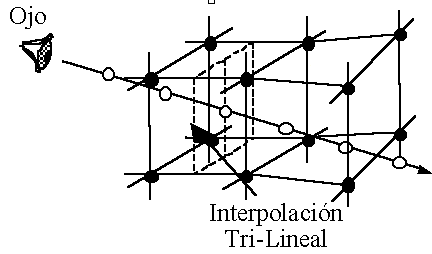
Ray Casting basado en celdas: (interpolación trilineal, luego los algoritmos son más complejos y costosos, pero con mayor calidad).- Ray tracing de celdas (composición BTF de
contribuciones, Phong y gradientes).
- Ray casting basado en celdas (visibilidad en el espacio
de la imagen, menor calidad, y mayor rapidez).
- Procesamiento Cell by Cell (híbrido,
mejor calidad, similar a splatting).
- Ray tracing de celdas (composición BTF de
contribuciones, Phong y gradientes).
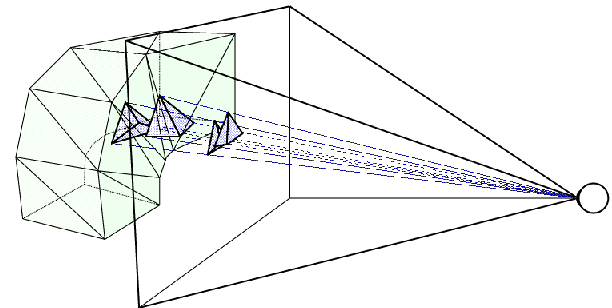
Características principales:
- Fácilmente paralelizables a nivel de datos.
- Propagan cada muestra de entrada en varias de salida.
- Permiten generar imágenes progresivas.
- Permiten visualizar resultados intermedios.
- Permiten aplicar algún tipo de coherencia.
La recorrida de los datos puede ser:
- Por proyecciones.
- Por funciones transformadas.
Métodos forward mapping proyectivos (renderizan por composición sobre un frame buffer).
- Proyección de voxels:
Front-to-back. (primitivos y con soporte para transparencias).
Splatting (contribución ponderada de un voxel en varios pixels).
Splatting jerárquico (representación piramidal de datos, permite precisión variable).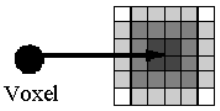
El splatting de un voxel produce una huella o footprint en varios pixels de la pantalla.
- Proyección de celdas:(clases de equivalencias
y coherencia).
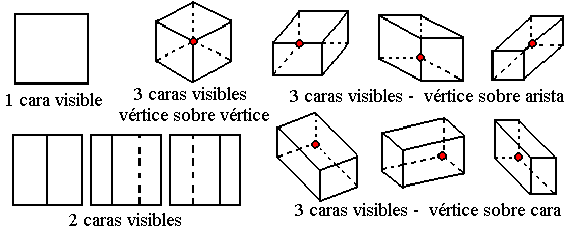
Casos posibles de proyección de celdas hexaédricas.
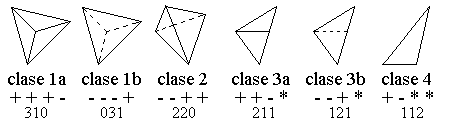
Casos posibles de proyección de celdas tetraédricas.
- Proyección de planos: (Rapidez y calidad.
Proyección eficiente debido a que hacen una
factorización de la transformación de viewing).
El método más utilizado es el Shear-Warp.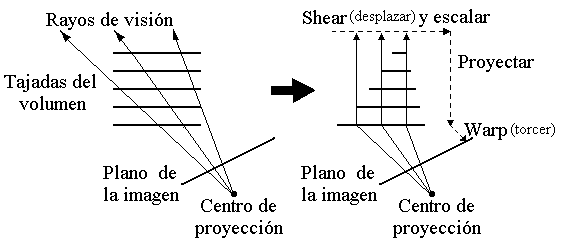
Métodos en dominios intermedios. (Datos-Dominio intermedio-Procesamiento)
- Dominio de Frecuencia (simplifica la proyección del volumen)
- Dominio de Compresión (menos almacenamiento y cálculos)
- Dominio de Wavelet (forma elegante de trabajar con multiresolución)